Обзор задачника «Алгебра. 10 класс» Мордкович (Профильный уровень)
Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
Особенности задачника
Одной из главных особенностей задачника является его структурированность и ориентация на постепенное усложнение материала. Учебник позволяет ученикам не только закрепить базовые знания, но и развить аналитическое мышление за счёт решения сложных задач.
Авторы уделяют большое внимание логике изложения: каждый новый раздел начинается с теоретической части, где подробно объясняются основные понятия и методы, а затем следуют задания с возрастающим уровнем сложности. Это делает процесс обучения комфортным и последовательным.
Преимущества
- Разнообразие заданийВ задачнике представлены задачи разного уровня сложности — от базовых до олимпиадных. Это позволяет использовать книгу как для текущей учёбы, так и для подготовки к экзаменам.
- Пошаговое обучениеМатериал изложен таким образом, что каждый новый раздел основывается на ранее изученном. Это помогает ученикам лучше усваивать сложные темы.
- Практическая направленностьЗадачи часто связаны с реальными примерами, что делает процесс обучения более интересным и прикладным.
- Подготовка к ЕГЭКнига идеально подходит для подготовки к профильной части Единого государственного экзамена по математике, так как включает задания, аналогичные тем, что встречаются на экзамене.
- Дополнительные материалыВ конце книги часто можно найти ответы или указания к решению сложных задач, что помогает ученикам проверять себя и понимать ошибки.
Недостатки
Несмотря на множество плюсов, у задачника есть и свои минусы. Например, некоторые темы могут быть изложены слишком кратко, что требует от ученика дополнительных усилий для понимания. Также сложные задачи без подробных решений могут вызывать трудности у тех, кто изучает материал самостоятельно.
Итог
Задачник Мордковича — это отличный выбор для школьников, которые хотят углубить свои знания по алгебре и успешно подготовиться к экзаменам. Книга сочетает в себе доступность, логичность и разнообразие заданий, что делает её универсальным инструментом для обучения.
Если вы ищете учебное пособие, которое поможет вам освоить сложные темы алгебры, этот задачник — именно то, что нужно!
ГДЗ по Алгебре 10 Класс Номер 5.5 Профильный Уровень Мордкович — Подробные Ответы
Ha числовой прямой отметьте все такие точки x, которые удовлетворяют заданному соотношению:
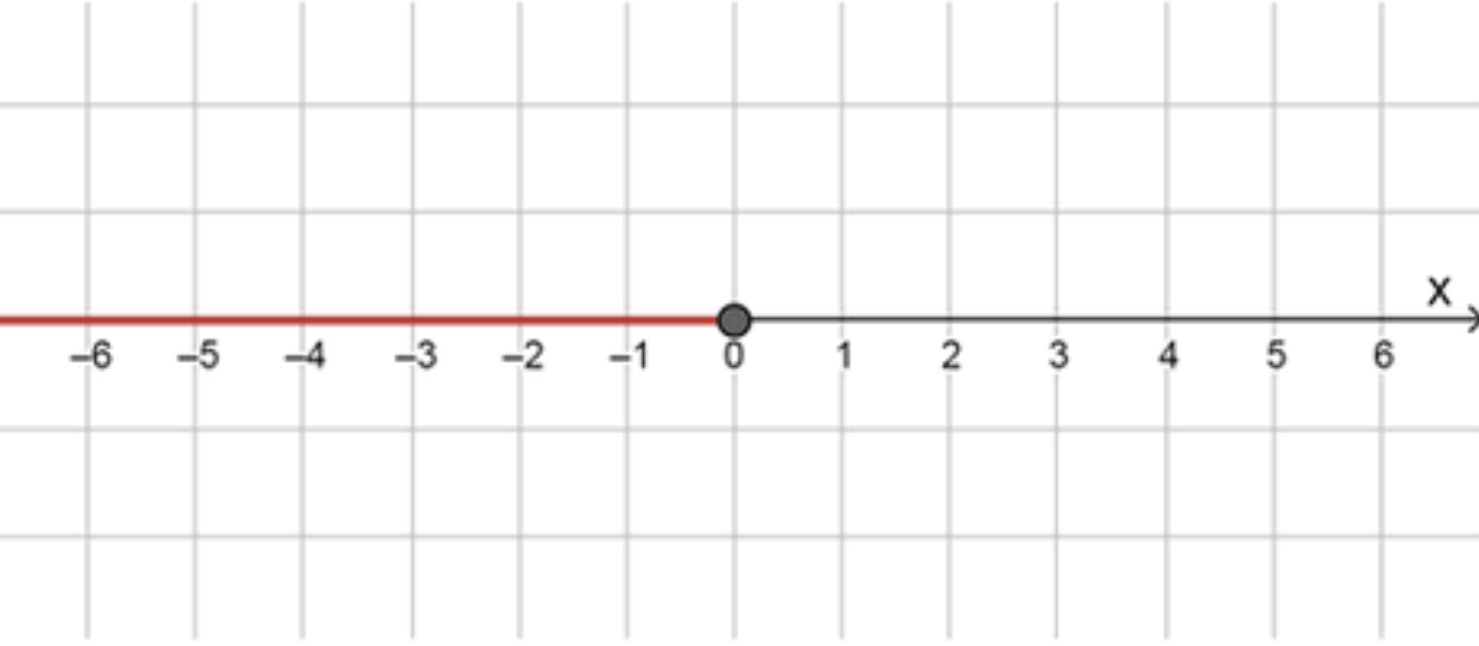
а) |x| = -x;
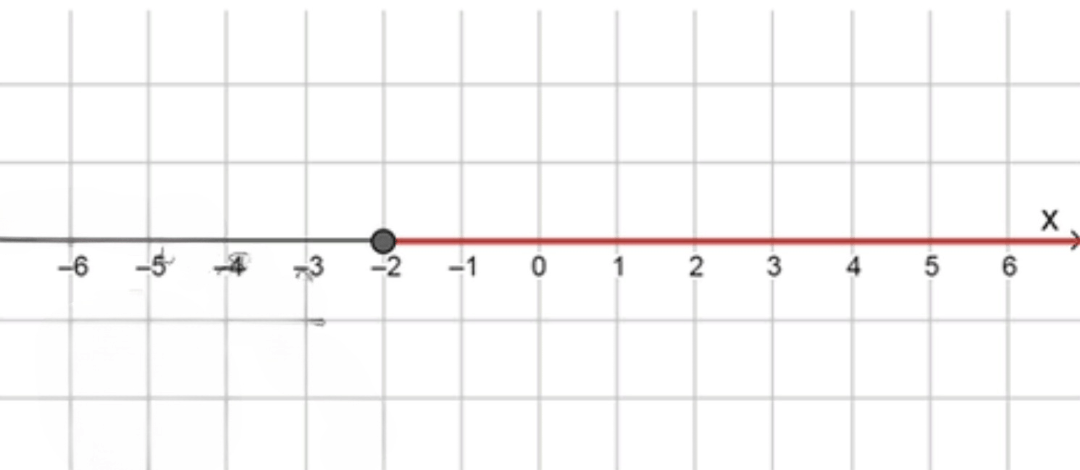
б) |х + 2| = x + 2;
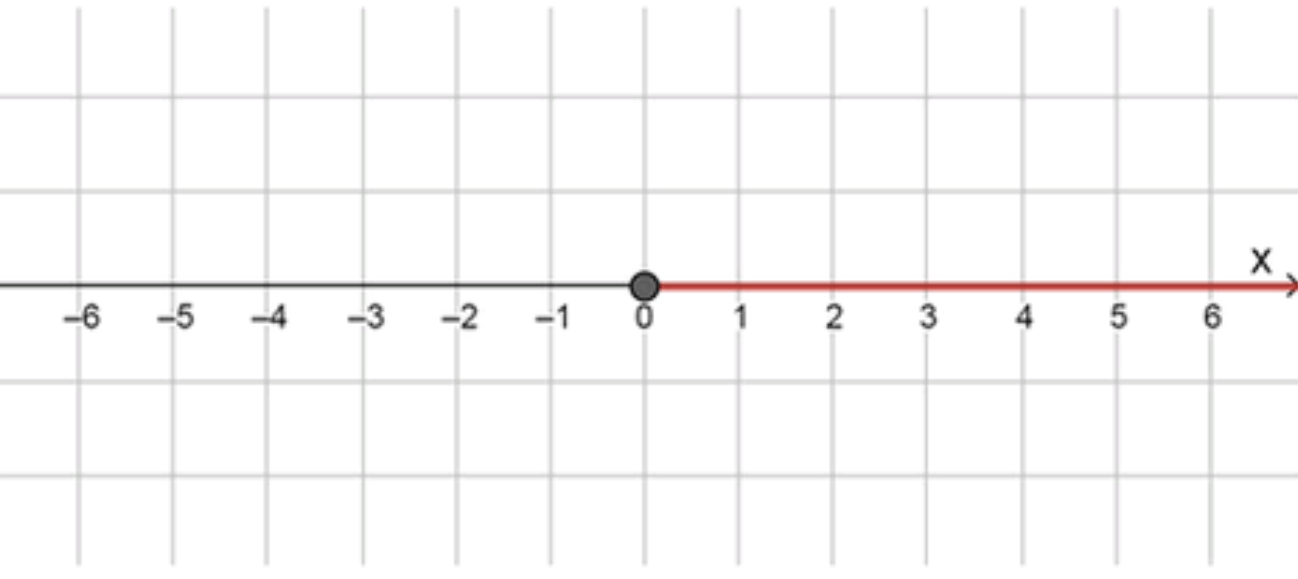
в) |x| = x;
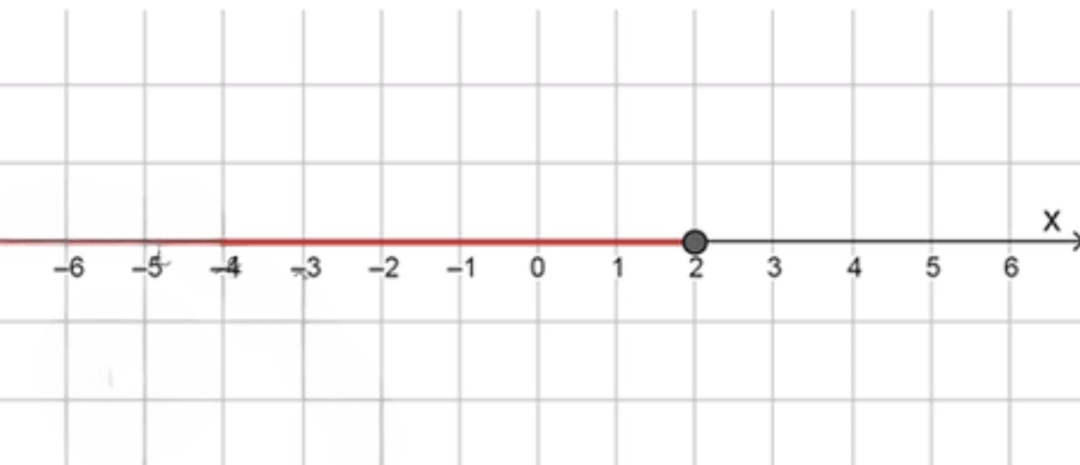
г) |x — 2| = 2 — x.
а) ;
- По определению модуля числа:
- На числовой прямой:
б) ;
- По определению модуля числа:
- На числовой прямой:
в) ;
- По определению модуля числа:
- На числовой прямой:
г) ;
- По определению модуля числа:
- На числовой прямой:
а)
Шаг 1: Разбор определения модуля числа
Модуль числа определяется как:
Нам дано уравнение , и нужно выяснить, при каких значениях оно выполняется.
Шаг 2: Анализ уравнения
- Если , то по определению модуля . Но в этом случае уравнение возможно только при , так как для положительных значений уравнение не выполняется.
- Если , то по определению модуля . В этом случае уравнение выполняется для всех отрицательных значений .
Шаг 3: Ответ
Таким образом, уравнение выполняется при всех .
Ответ: .
б)
Шаг 1: Разбор определения модуля числа
Модуль числа можно записать по определению как:
Нам дано уравнение , и нужно выяснить, при каких значениях оно выполняется.
Шаг 2: Анализ уравнения
- Если , то по определению модуля , и уравнение выполняется для всех .
- Если , то по определению модуля , и уравнение приводит к противоречию, потому что не имеет решения.
Шаг 3: Ответ
Таким образом, уравнение выполняется при .
Ответ: .
в)
Шаг 1: Разбор определения модуля числа
Модуль числа определяется как:
Нам дано уравнение , и нужно выяснить, при каких значениях оно выполняется.
Шаг 2: Анализ уравнения
- Если , то по определению модуля , и уравнение выполняется для всех .
- Если , то по определению модуля , и уравнение приводит к противоречию, так как для отрицательных это не возможно.
Шаг 3: Ответ
Таким образом, уравнение выполняется только при .
Ответ: .
г)
Шаг 1: Разбор определения модуля числа
Модуль числа определяется как:
Нам дано уравнение , и нужно выяснить, при каких значениях оно выполняется.
Шаг 2: Анализ уравнения
Если , то по определению модуля , и уравнение преобразуется в:
Если , то по определению модуля , и уравнение преобразуется в:
что является тождеством и выполняется для всех .
Шаг 3: Ответ
Таким образом, уравнение выполняется для всех .
Ответ: .
Алгебра