Обзор задачника «Алгебра. 10 класс» Мордкович (Профильный уровень)
Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
Особенности задачника
Одной из главных особенностей задачника является его структурированность и ориентация на постепенное усложнение материала. Учебник позволяет ученикам не только закрепить базовые знания, но и развить аналитическое мышление за счёт решения сложных задач.
Авторы уделяют большое внимание логике изложения: каждый новый раздел начинается с теоретической части, где подробно объясняются основные понятия и методы, а затем следуют задания с возрастающим уровнем сложности. Это делает процесс обучения комфортным и последовательным.
Преимущества
- Разнообразие заданийВ задачнике представлены задачи разного уровня сложности — от базовых до олимпиадных. Это позволяет использовать книгу как для текущей учёбы, так и для подготовки к экзаменам.
- Пошаговое обучениеМатериал изложен таким образом, что каждый новый раздел основывается на ранее изученном. Это помогает ученикам лучше усваивать сложные темы.
- Практическая направленностьЗадачи часто связаны с реальными примерами, что делает процесс обучения более интересным и прикладным.
- Подготовка к ЕГЭКнига идеально подходит для подготовки к профильной части Единого государственного экзамена по математике, так как включает задания, аналогичные тем, что встречаются на экзамене.
- Дополнительные материалыВ конце книги часто можно найти ответы или указания к решению сложных задач, что помогает ученикам проверять себя и понимать ошибки.
Недостатки
Несмотря на множество плюсов, у задачника есть и свои минусы. Например, некоторые темы могут быть изложены слишком кратко, что требует от ученика дополнительных усилий для понимания. Также сложные задачи без подробных решений могут вызывать трудности у тех, кто изучает материал самостоятельно.
Итог
Задачник Мордковича — это отличный выбор для школьников, которые хотят углубить свои знания по алгебре и успешно подготовиться к экзаменам. Книга сочетает в себе доступность, логичность и разнообразие заданий, что делает её универсальным инструментом для обучения.
Если вы ищете учебное пособие, которое поможет вам освоить сложные темы алгебры, этот задачник — именно то, что нужно!
ГДЗ по Алгебре 10 Класс Номер 4.12 Профильный Уровень Мордкович — Подробные Ответы
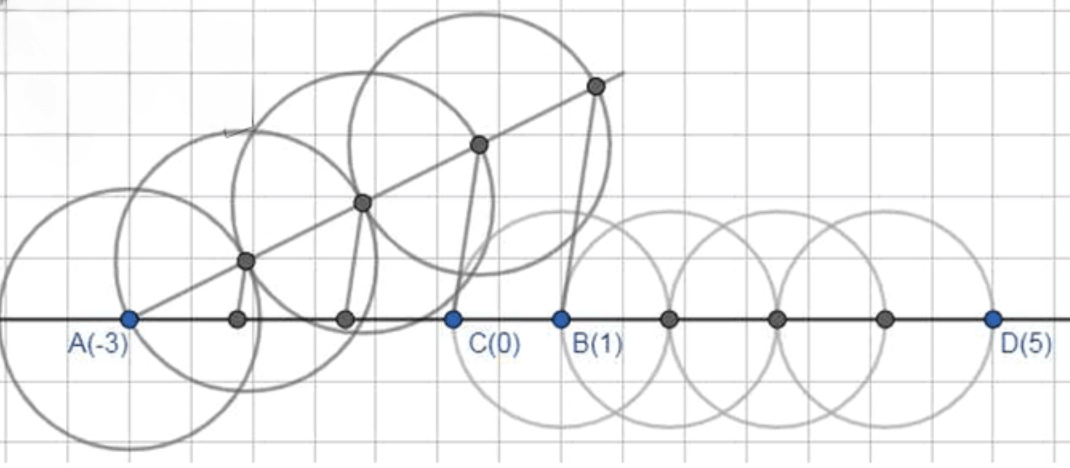
а) На числовой прямой отмечены точки и . При помощи циркуля и линейки постройте точки и .
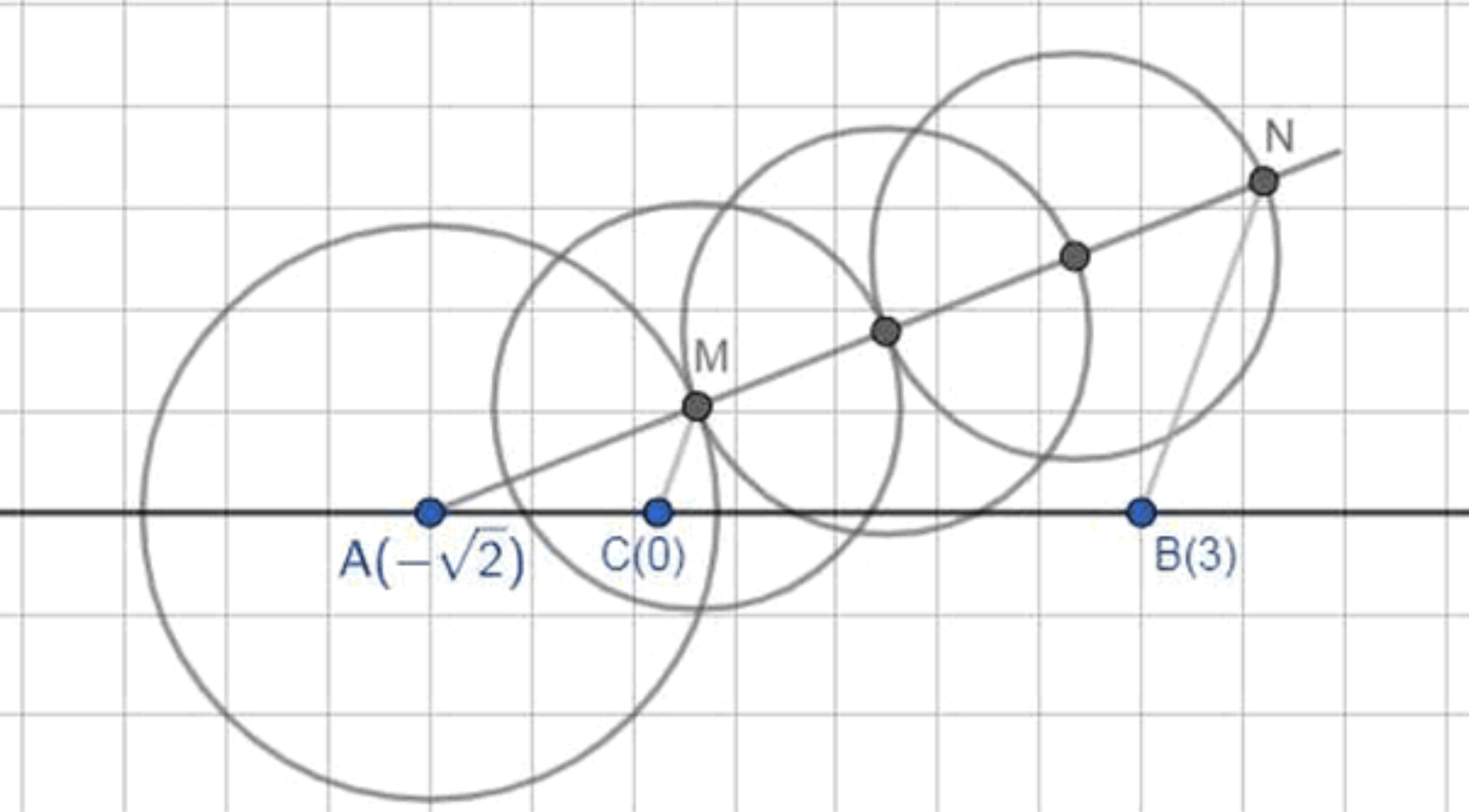
б) На числовой прямой отмечены точки и . При помощи циркуля и линейки постройте точку .
а) На числовой прямой отмечены точки и , требуется отметить точки и при помощи циркуля и линейки;
1. Разделим отрезок на четыре равные части, для чего:
- Проведем из точки произвольный луч;
- Отложим последовательно на этом луче 4 равных отрезка;
- От конца последнего отрезка проведем прямую через точку ;
- Через концы других отрезков проведем параллельные ей прямые;
2. Каждый из этих отрезков является единичным:
3. От точки отложим один единичный отрезок влево и четыре единичных отрезка вправо:
б) На числовой прямой отмечены точки и , требуется отметить точку ;
1. Возьмем произвольный единичный отрезок;
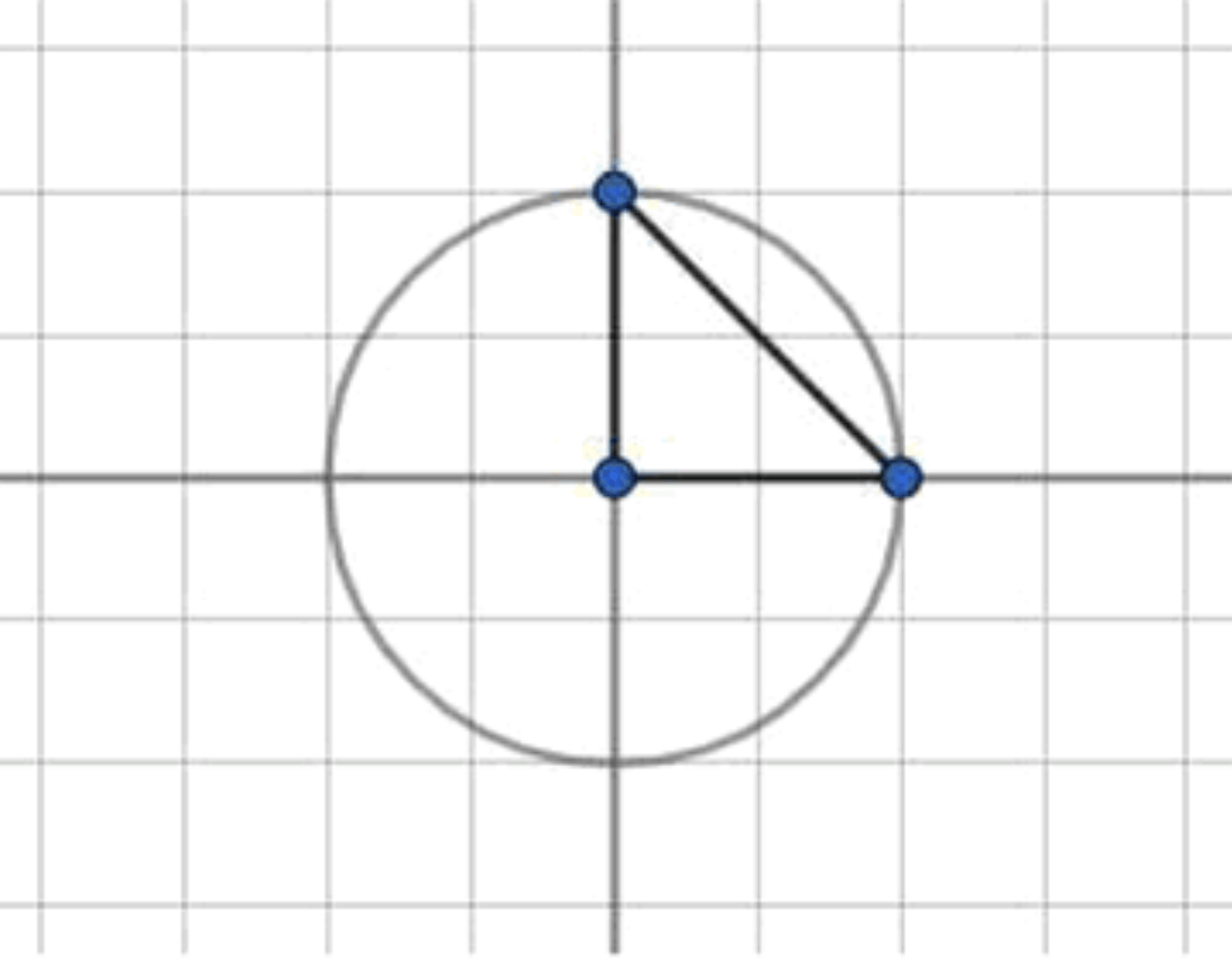
2. Построим прямоугольный треугольник с катетами:
3. Проведем из точки произвольный луч;
4. На этом луче отложим отрезок длины ;
5. Отложим на луче от точки последовательно три единичных отрезка, конец последнего из них обозначим буквой ;
6. Проведем прямую и параллельную ей прямую , которая пересечет числовую прямую в точке :
7. По теореме о пропорциональных отрезках:
Часть а)
Задание: На числовой прямой отмечены точки и , требуется отметить точки и при помощи циркуля и линейки.
Шаг 1: Разделение отрезка на 4 равные части
Определим длину отрезка :
- Точки и имеют координаты и .
- Длина отрезка вычисляется как разность координат и :
- Длина отрезка равна 4 единицам.
Разделим отрезок на 4 равные части:
- Для того чтобы разделить отрезок на 4 равные части, нужно длину отрезка (равную 4) разделить на 4:
- Каждая из частей будет длиной 1 единица.
Построим разделение:
- Проведем из точки произвольный луч, который будет использоваться для отложения равных отрезков.
- С помощью циркуля отложим 4 равных отрезка длиной 1.
- Отложив 4 равных отрезка, получим точки, разделяющие отрезок на 4 части.
- После этого, используя линейку, соединяем последнюю точку с точкой .
- Параллельно этой прямой через другие точки проведем прямые, которые также будут разделять отрезок на равные части.
Шаг 2: Длины отрезков
Каждый из этих отрезков будет иметь длину:
Таким образом, длина каждого отрезка разделяющего на 4 части, равна 1.
Шаг 3: Отложение единичных отрезков от точки
От точки отложим 1 единичный отрезок влево.
- Для этого мы отложим отрезок длиной 1 единица влево от точки . Точка, которая будет находиться на расстоянии 1 единица влево от точки , будет точкой с координатой .
Отложим 4 единичных отрезка вправо.
- Теперь, от точки откладываем 4 отрезка длиной 1 единица вправо. Это приведет к тому, что мы получим точку с координатой 5.
Часть б)
Задание: На числовой прямой отмечены точки и , требуется отметить точку .
Шаг 1: Построение прямоугольного треугольника с катетами
Построим прямоугольный треугольник с катетами:
- Нам нужно построить прямоугольный треугольник с катетами длины 1, чтобы найти гипотенузу.
- По теореме Пифагора длина гипотенузы равна:
- Таким образом, гипотенуза будет иметь длину .
Шаг 2: Откладывание отрезка длины
Отложим отрезок длины вправо от точки .
- На числовой прямой точка имеет координату , и отложив от этой точки отрезок длины , мы получим точку с координатой 0, так как:
- Это точка .
Шаг 3: Отложение единичных отрезков
Отложим на луче от точки 3 единичных отрезка.
- От точки отложим 3 единичных отрезка длиной 1, и конечная точка будет точкой , которая будет находиться на координате 3.
Шаг 4: Прямая через точки и
Проводим прямую .
- Теперь проведем прямую через точку и точку , которая будет проходить через обе эти точки.
Проводим параллельную прямую .
- Параллельно прямой проводим прямую через точку , и эта прямая пересечет числовую прямую в точке .
Шаг 5: Применение теоремы о пропорциональных отрезках
По теореме о пропорциональных отрезках:
Алгебра