ГДЗ по Алгебре 10 Класс Номер 2.18 Профильный Уровень Мордкович — Подробные Ответы

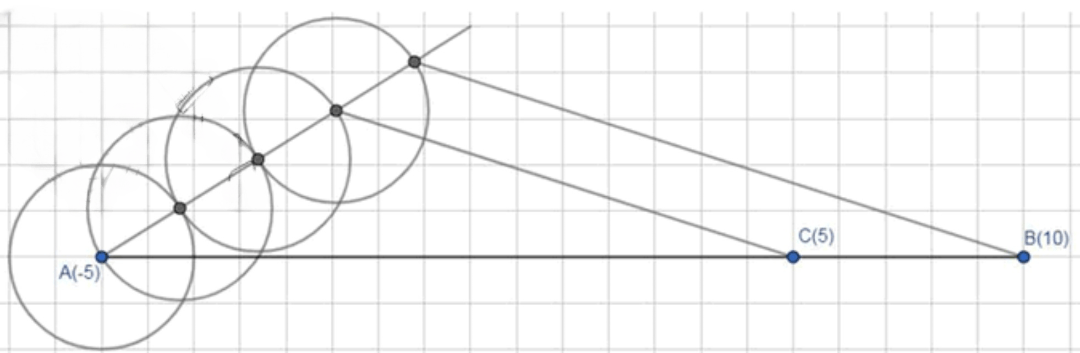
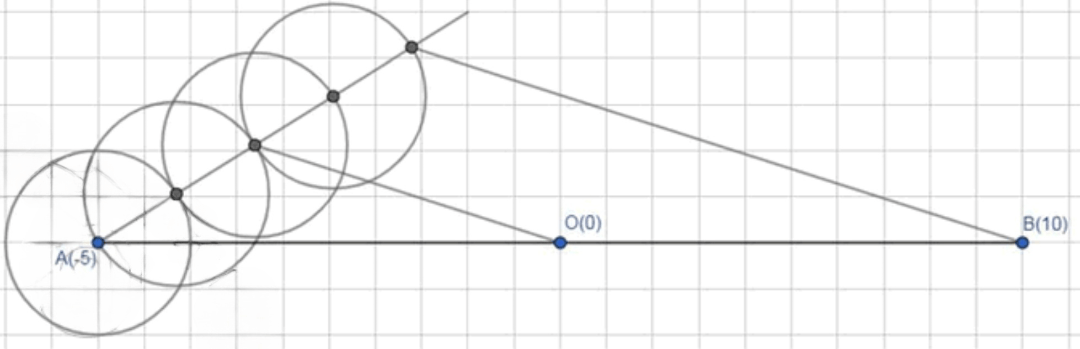
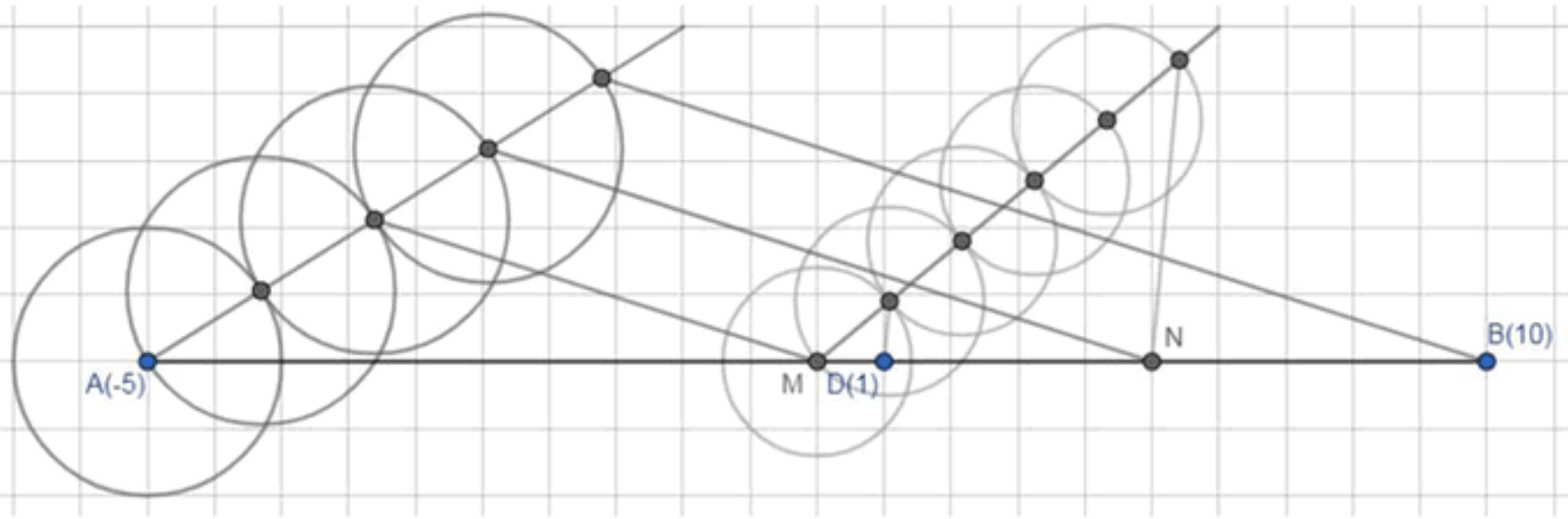
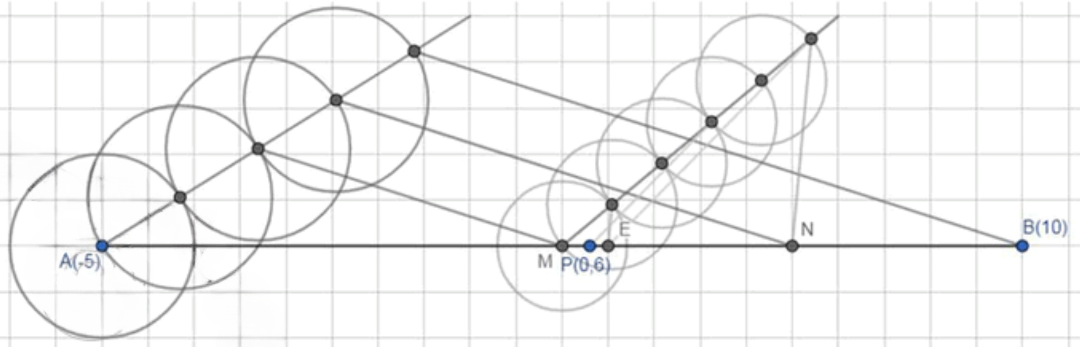
Ha числовой прямой отмечены точки A(-5) и B(10). C помощью циркуля и линейки отметьте точку:

a) C(5);

б) O(0);

в) D(1);

г) P(0,6).

Чтобы разделить отрезок на $n$ равных частей требуется:

• Провести произвольный луч из одного конца отрезка;
• На этом луче отмерить с помощью циркуля $n$ равных частей;
• Из последней отмеченной точки провести прямую к другому концу данного отрезка, а затем из каждой точки на луче провести прямые, параллельные этой прямой;

На числовой прямой отмечены точки $A(-5)$ и $B(10)$, отметить:

а) Точку $C(5)$;

1. Разделим отрезок $AB$ на 4 равные части;
2. Конец третьего отрезка является искомой точкой:

б) Точку $O(0)$;

1. Разделим отрезок $AB$ на 4 равные части;
2. Конец второго отрезка является искомой точкой:

в) Точку $D(1)$;

1. Разделим отрезок $AB$ на 4 равные части;
2. Отметим точками $M$ и $N$ концы второго и третьего отрезка;
3. Разделим отрезок $MN$ на 5 равных частей;
4. Конец первого отрезка является искомой точкой:

г) Точку $P(0,6)$;

1. Разделим отрезок $AB$ на 4 равные части;
2. Отметим точками $M$ и $N$ концы второго и третьего отрезка;
3. Разделим отрезок $MN$ на 5 равных частей;
4. Отметим точкой $E$ конец первого отрезка;
5. Разделим отрезок $ME$ на 5 равных частей;
6. Конец третьего отрезка является искомой точкой:

Общие шаги для всех пунктов задачи

1. Начало:
   На числовой прямой отмечены две точки $A(-5)$ и $B(10)$. Мы хотим разделить отрезок $AB$ на несколько равных частей и найти определенные точки, лежащие на этом отрезке.
2. Разделение отрезка на равные части:
   Для того чтобы разделить отрезок на равные части, проведем произвольный луч из одной из точек, например, из точки $A$. Затем с помощью циркуля отмерим $n$ равных частей на этом луче (где $n$ — количество частей, на которое нужно разделить отрезок). На последнем шаге мы соединяем точки, чтобы провести прямые, параллельные отрезку $AB$, через все отмеченные на луче точки.

Теперь давайте разберем каждый конкретный пункт задачи.

а) Точку $C(5)$

Шаг 1: Разделим отрезок $AB$ на 4 равные части.

• Чтобы разделить отрезок $AB$ на 4 равные части, проводим произвольный луч из точки $A$, используя циркуль для отмеривания 4 равных частей.
• Нам нужно найти точку, которая находится через 3/4 отрезка от точки $A$ (конец третьего отрезка будет нужной точкой).

Шаг 2: Находим точку $C$.

• Конец третьего отрезка от точки $A$ будет точкой $C(5)$, поскольку на числовой прямой, между точками $A(-5)$ и $B(10)$, точка $C(5)$ находится на 3/4 пути от $A$ к $B$.

Ответ: Точка $C$ будет на отрезке $AB$ и будет иметь координаты $C(5)$.

Изображение:

б) Точку $O(0)$

Шаг 1: Разделим отрезок $AB$ на 4 равные части.

• Точно так же, как в предыдущем пункте, мы делим отрезок $AB$ на 4 равные части.

Шаг 2: Находим точку $O$.

• Точка $O(0)$ — это точка, которая находится на середине отрезка $AB$, то есть на 2/4 пути от $A$ к $B$. Это означает, что точка $O$ делит отрезок $AB$ пополам.
• Точка $O(0)$ является концом второго отрезка, так как на 2/4 отрезка от $A$ к $B$ будет расположена точка с координатой $0$.

Ответ: Точка $O$ имеет координаты $O(0)$.

Изображение:

в) Точку $D(1)$

Шаг 1: Разделим отрезок $AB$ на 4 равные части.

• Сначала разделяем отрезок $AB$ на 4 равные части, используя циркуль, как в предыдущих пунктах.

Шаг 2: Отметим точками $M$ и $N$ концы второго и третьего отрезков.

• Отметим точку $M$ как конец второго отрезка и точку $N$ как конец третьего отрезка. Эти точки находятся на отрезке $AB$.

Шаг 3: Разделим отрезок $MN$ на 5 равных частей.

• Теперь, разделив отрезок $MN$ на 5 равных частей, мы отмеряем, что каждая часть составляет $\frac{1}{5}$ длины отрезка $MN$.

Шаг 4: Находим точку $D(1)$.

• Конец первого отрезка из разделенного отрезка $MN$ будет точкой $D(1)$, так как точка $D$ находится на числовой прямой, в точке с координатой 1.

Ответ: Точка $D$ будет на отрезке $AB$, и ее координаты $D(1)$.

Изображение:

г) Точку $P(0,6)$

Шаг 1: Разделим отрезок $AB$ на 4 равные части.

• Разделим отрезок $AB$ на 4 равные части.

Шаг 2: Отметим точками $M$ и $N$ концы второго и третьего отрезков.

• Отметим точку $M$ как конец второго отрезка и точку $N$ как конец третьего отрезка.

Шаг 3: Разделим отрезок $MN$ на 5 равных частей.

• Теперь разделим отрезок $MN$ на 5 равных частей. Это даст нам равные интервалы на отрезке $MN$.

Шаг 4: Отметим точкой $E$ конец первого отрезка.

• Отметим точку $E$, которая будет концом первого отрезка из разделенного отрезка $MN$.

Шаг 5: Разделим отрезок $ME$ на 5 равных частей.

• Далее разделим отрезок $ME$ на 5 равных частей.

Шаг 6: Находим точку $P(0,6)$.

• Конец третьего отрезка из разделенного отрезка $ME$ будет точкой $P(0,6)$, так как это искомая точка на числовой прямой.

Ответ: Точка $P$ будет иметь координаты $P(0,6)$.

Изображение:

Итог:

1. Точка $C(5)$: Разделяем отрезок $AB$ на 4 равные части и находим конец третьего отрезка.
2. Точка $O(0)$: Разделяем отрезок $AB$ на 4 равные части и находим конец второго отрезка.
3. Точка $D(1)$: Разделяем отрезок $AB$ на 4 равные части, затем делим отрезок $MN$ на 5 равных частей.
4. Точка $P(0,6)$: Разделяем отрезок $AB$ на 4 равные части, затем разделяем отрезок $MN$ и $ME$ на 5 равных частей.